Telescope Equations
Resolving Power of a Telescope
Theory
Interference Pattern
Light, as you may know, travels in the form of waves. When
the waves pass through the opening of your telescope, the disruption causes
the waves to run into each other. Where the crossed waves match peak to
peak and trough to trough, the waves reinforce each other and get bright.
Where the peaks of one wave hit the troughs of the other, they cancel each
other out and get dark. The resulting dark and light pattern is called an
interference pattern.
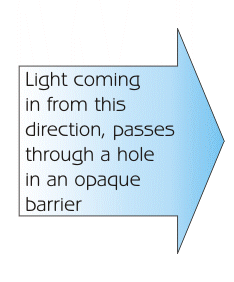
|  |
Waves, coming in from the left, and passing through a hole.
Notice how the waves that go straight through the hole are
brighter, and as the angle from the centerline goes up or
down, you can see the waves get alternately darker and
brighter. That's the interference pattern.
The hole represents the opening of your telescope.
|
Airy Disk

So now in the case of your telescope the circular opening of the
telescope creates a circular interference pattern.
Because of this interference pattern, when you make an image of a star,
it does NOT focus to a perfect point. Rather, it focuses to a disk, and if
you set your telescope for high magnification and examine the image carefully,
you can see that there is a disk with faint rings around it -- this is the
interference pattern that is caused by the circular aperture of your telescope.
In fact, this is a special interference pattern and it has a special name --
the "Airy disk" -- named after Sir George Biddell Airy, an English astronomer
who described this pattern mathematically in 1834.
 |
 |
| Idealized picture of Airy disk |
Two close stars appear as two Airy disks. |
 |
 |
| When the two stars start getting as close together as the
radius of the Airy disk, we start to have trouble telling
them apart. |
When the two stars are closer together than the radius of the
Airy disk, we can no longer tell them apart. |
 |
 |
| How a star's Airy disk looks in a telescope (due to
atmospheric disturbance) |
Epsilon Boötis, a very close double star
at 2.8 arc-seconds in the constellation
Boötes, is split here at
high power, revealing the beauty of this blue and yellow pair,
and also clearly showing the diffraction rings, very much as
they appear in the eyepiece. This excellent photo courtesy of
Damian Peach. |
Diffraction Limit
The bending of light which causes this interference pattern is known as
"diffraction", and the Airy disk is also known as the diffraction pattern of
the scope.
The radius of the central disk of this pattern, in radians -- let's call
it "R" -- is given by the formula
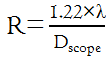
where λ is the wavelength of light,
which happens to be 550x10-9m for green light, and Dscope
is the diameter of the objective in meters (so really the same thing as
DO, but to emphasize this is in meters, not millimeters).
With regard to your telescope, what is important in this equation is that
the size of the Airy disk depends on the diameter of the objective ONLY, and
as the diameter of the objective gets bigger, the Airy disk gets smaller.
This means as the diameter of your scope gets bigger, you can see smaller
and smaller detail -- or equivalently, you can split stars that are closer
together. Conversely, this means that there is a limit to the detail you
can see with your scope. That limit is dictated ENTIRELY by the diameter
of the scope, and it is due to the diffraction effects caused by the scope
opening.
For this reason, the radius of the Airy disk, as calculated above, is
known as the "diffraction limit". Note then that when you can see
the rings of the Airy Disk, this signals to you that you are operating at
the limit of the scope's power to resolve detail.
Dawes Limit
The diffraction limit equation gives an answer in radians, whereas most
dimensions in astronomy are given in degrees, minutes, or seconds of arc.
Also because of various other factors, the actual limit of detail that an
observer can see does not match exactly to the diffraction limit. Interestingly,
a skilled observer can do better than the diffraction formula would suggest.
In 1867, William Rutter Dawes determined the practical limit on resolving
power for a telescope, known as the Dawes limit. Dawes expressed this as the
closest that two stars could be together in the sky and still be seen as two
stars. The Dawes Limit is 4.56 seconds of arc, divided by the telescope
aperture in inches. We can multiply the Dawes limit by 25.4 to convert to the
metric system (in mm), which gets you to 115.8, and then round to a number that
is more convenient when doing the math in your head , and we get the resolving
power of the scope, PR in seconds of arc.
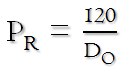
Don't Forget the Air
You're not just looking through your telescope at the stars, you're also
looking through air -- literally tons of air. 50 miles of it straight up,
and hundreds of miles when you're looking close to the horizon. That air
is usually in motion, and the shifting masses of air at different temperatures
cause the light to deflect. The deflection is small and subtle, but when
you are looking at high magnification, it seriously affects the amount of
detail you are able to see.
Atmospheric conditions for astronomical viewing are talked about in terms
of "transparency" and "seeing".
The term "transparency" refers to how clear the sky appears to be. It is
measured in terms of the faintest stars you can see by eye. So for example
in my neighborhood it is not unusual to have a
magnitude 3 night -- you can't
even see stars that are magnitude 4 -- but on a really good night you can just
see magnitude 5 stars. Transparency is determined by the combination of lights
that brighten the sky and water vapor or dust in the air to catch the light
and obscure faint stars and deep sky objects.
The peculiar term "seeing" refers to how steady the air is. This
directly affects the detail that you can resolve. The more turbulent the
air, the worse the resolution. A typical sky only permits 2-3 arc-seconds
of resolution, whereas a good sky, at sea level, will permit closer to 1
arc-second. A superb sky at high altitude, could possibly provide 0.4
arc-second seeing.
Let's translate that into terms of magnification. As discussed on the
Maximum Magnification page, the
resolving power of your eye, assuming 20/20 vision, is 120 arc-seconds.
If the atmosphere will permit 1 arc-second resolution, how much do I need
to magnify that to make it 120 arc-seconds? By what factor do I multiply
1 in order to get 120? Take your time... that's right, 120.
What that really means to us is that as you increase magnification above
120, your eye starts to see the blurring the atmosphere introduces.
Remember, this is when we have good atmospheric seeing, on some
nights the image can start to get blurred as you get above a magnification
of 60 or so. Then we can certainly say that as you get to the range of
magnification of 150-200, the atmosphere will limit what you can resolve.
Any further increase in magnification will only give you a closer more
detailed look at exactly how the atmosphere is blurring and distorting
the image.
Bearing in mind the fact that the
maximum magnification of a scope is simply the diameter of the scope
in millimeters, we can very quickly determine what scopes will be limited
by the atmosphere. If we consider the upper limit imposed by the atmosphere
to be a magnification of 200, then 200mm translates into an 8 inch scope.
So then if you're wondering why anyone would get a scope larger than, say,
8 inches... the answer is that resolving power is only part of the
picture. Image brightness is also driven primarily by the scope diameter,
as you can see in the pages on Magnitude Gain
and on Surface Brightness.
Practice
Splitting the Double Double
Epsilon Lyrae is a famous star, known as "the Double Double", in the
constellation Lyra.
This star shows as a double star when you look at it in binoculars. But then
if you look at it in a telescope, and if the telescope is big enough, you can
see that each of the two stars of this double is also a double!
So here's the question: does my 90mm, f/13.9 Meade ETX telescope have the
resolving power to split the Double Double?
First we look up the Double Double, or Epsilon Lyrae, in a reference like
Burnham's Celestial Handbook or find it on the web on a page like the one
by Professor James
Kaler. Prof. Kaler's page tells us that one pair is 2.8 arc-seconds apart,
the other is 2.2, consistent with what Burnham's handbook says.
Then let's see what the resolving power of my ETX ought to be:
the Dawes Limit formula says
PR= 120/DO
So I only need to know the diameter of the objective, or DO,
for my ETX to figure this one out. Since, as I noted earlier, DO
= 90 mm, then PR = 120/90 = 1.33 seconds of arc. Since
that is smaller than the separation of the components of Epsilon Lyrae, I
should be able to split the Double Double with my scope.
I can report to you that in fact I have been able to split the Double
Double with my ETX, which speaks well of the optics on my ETX. I can also
report that it requires good atmospheric conditions.
That's because, as noted above, the atmosphere will limit you to 1 second
of arc on a good night, and worse than that on most nights. So while my ETX
can split the Double Double, it can't do it every night. But
then neither can the bigger scopes -- we all need a clear, steady sky to
bag the Double Double.

Notice how the two pairs align at right angles to each other --
one pair aligns North-South, and the other aligns East-West.
It's very cool to get this in the eyepiece. These four stars
form a set that is a true double-double star, formed from the
same nebula, which was spinning so fast it first spun apart
into two protostars. They in turn each spun themselves apart
into two stars. Today, the two spinning pairs are still
orbiting each other. This exceptionally clear photo of the
Double Double courtesy of
Damian Peach.
 Back to Telescope Equations Home Page
Back to Telescope Equations Home Page
Questions
Your questions and comments regarding this page are welcome.
You can e-mail Randy Culp for inquiries,
suggestions, new ideas or just to chat.
Updated 15 November 2012









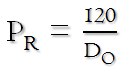


 Back to Telescope Equations Home Page
Back to Telescope Equations Home Page